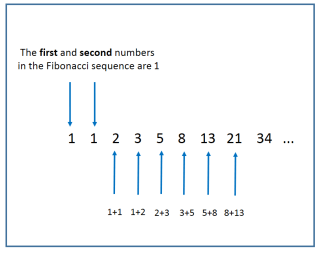
The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding ones, usually starting with 0 and 1. The sequence goes 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. The Fibonacci sequence has many interesting properties and is found in many areas of mathematics, as well as in nature.
To write a program in Java that generates the Fibonacci sequence, we can use a for loop and an array to store the sequence. Here is an example of such a program:
public class Fibonacci {
public static void main(String[] args) {
int n = 10;
int[] fib = new int[n];
fib[0] = 0;
fib[1] = 1;
for(int i = 2; i < n; i++) {
fib[i] = fib[i-1] + fib[i-2];
}
for(int i = 0; i < n; i++) {
System.out.print(fib[i] + " ");
}
}
}
In this program, we first declare a variable n that determines the number of terms in the Fibonacci sequence that we want to generate. We then create an array fib of size n to store the sequence. We initialize the first two terms of the sequence, 0 and 1, in the first and second elements of the array, respectively.
Next, we use a for loop to generate the remaining terms of the sequence. We start the loop at 2 because the first two terms have already been initialized. In each iteration of the loop, we calculate the next term in the sequence by adding the previous two terms and store it in the array.
Finally, we use another for loop to print out the terms of the sequence stored in the array. When you run the code, you’ll see the output is “0 1 1 2 3 5 8 13 21 34” which is the first 10 numbers of fibonacci series.
This is just one way to write a program to generate the Fibonacci sequence in Java. There are many other ways to do it, depending on your specific needs and constraints.
It’s also worth noting that, for large values of n, this implementation will be quite slow due to the use of a for loop and the fact that it recalculates the same values multiple times. In those cases, it would be better to use a more efficient algorithm such as the matrix exponentiation method which is a O(log n) algorithm.